Приложение
к задачам по спецкурсу «Теория реакционной способности органических соединений»

1. Справочник химика, том III, с. 935-937

Реакционная способность органических соединений

Таблицы данного раздела предназначены для вычисления констант равновесия и скоростей реакций органических соединений, а также потенциалов полуволн их полярографического восстановления.

Таблицы составлены на основании корреляционных уравнений Гаммета и Тафта и модификаций этих уравнений (В.А. Пальм, Успехи химии, 30, вып. 9, с.1069, 1961). Величины, приведенные в табл. 3–8, позволяют вычислить около миллиарда значений констант скоростей и равновесия реакций. Кроме того, по корреляционным уравнениям табл. 9, благодаря исключительной практической эффективности перекрестных корреляций, можно вычислить еще большее число констант.

Константы равновесия или скоростей реакций (или полярографические характеристики) могут быть вычислены путем подстановки приведенных в таблицах постоянных в соответствующие корреляционные уравнения. Эти постоянные подразделяются на два типа: одни характеризуют определенные классы реакций при данных условиях (реакционные серии), другие – структурные единицы (заместители). Степень соответствия определяемых по таблицам величин имеющимся экспериментальным данным характеризуется среднеквадратичным отклонением s точек для отдельных заместителей от линии регрессии. Степень приложимости указанного в табл. 8 или 9 корреляционного уравнения к соответствующей реакционной серии характеризуется корреляционным коэффициентом r. Условно можно принять, что при r ≥ 0,99 имеется отличная корреляция, при 0,99 > r ≥ 0,95 – хорошая корреляция, при 0,95 > r ≥ 0,90 – удовлетворительная и при r < 0,90 – неудовлетворительная корреляция.

С помощью приведенных здесь таблиц могут решаться и более сложные задачи. Так, можно рассчитать условия синтеза органических соединений, их устойчивость и т. п. (см. примеры, приведенные ниже).

Постоянные в табл. 3–7, характеризующие структурные единицы (заместители), могут быть использованы в целях определения по экспериментальным данным констант корреляционных уравнений для реакционных серий, не вошедших в настоящие таблицы. При этом вследствие неравноценности (с точки зрения строгости физического смысла) постоянных, приведенных в табл. 3–7, следует пользоваться только корреляционными уравнениями (1), (1а), (2), (2а), (6) и (6а), помещенными в преамбуле к табл. 8; уравнения (3) и (4) рекомендуется применять лишь в том случае, когда из табл. 4 используются только величины E_s^c или E_s^o.

Более подробно о рекомендуемых практических правилах применения корреляционных уравнений см. статью В.А. Пальма в сб. «Корреляционные уравнения в органической химии», т. II, Тарту, 1963.

Расчет искомых  величин  производится в следующем порядке.

 

Вычисление констант скоростей или равновесия реакций. В табл. 1 находят индекс основной реакционной серии, к которой относится искомая реакция. Каждый такой индекс состоит из порядкового номера и нуля (например, 22-0). Реакционные серии в табл. 1 расположены по возрастанию их индексов; для облегчения пользования этой таблицей она снабжена указателем, в котором приводятся интервалы порядковых номеров, соответствующие определенным группам реакций или реагентов.

В табл. 1 для каждой основной реакционной серии указан способ присоединения переменного заместителя (или заместителей) к реакционному центру. В табл. 2 приведены различные структурные единицы, которые могут быть расположены между реакционным центром и переменным заместителем; каждая из них имеет порядковый номер. Пользуясь этим номером, можно составлять индексы производных реакционных серий, соответствующих тем или иным основным реакционным сериям из табл. 1.

Например, основная реакционная серия диссоциации карбоновых кислот имеет индекс 1-0. Пусть нас интересует реакционная серия диссоциации мета- и пара-замещенных бензойных кислот. Структурная единица Z = фенилен имеет в табл. 2 порядковый номер 11. Следовательно, индекс искомой реакционной серии будет 1-11.

По установленному индексу реакционной серии находят в табл. 8 условия реакции (температура, растворитель), номер корреляционного уравнения и значения постоянных этого уравнения для данной реакционной серии; здесь же приводятся значения среднеквадратичных отклонений s и корреляционных коэффициентов r, характеризующих степень соответствия результатов расчетов имеющимся экспериментальным данным.

Корреляционное уравнение, номер которого установлен по табл. 8, находят по этому номеру в преамбуле к той же таблице. Исходя из строения рассматриваемого соединения, устанавливают, какая конкретная структурная единица соответствует заместителю X, и в табл. 3–7 находят значения тех постоянных для этого заместителя, которые требуются для расчета по корреляционному уравнению. Подставляя в корреляционное уравнение найденные величины, а также значения постоянных для реакционной серии из табл. 8, вычисляют искомую величину.

В некоторых случаях для расчета искомых величин следует пользоваться корреляционными уравнениями, приведенными в табл. 9. Все такие случаи указаны в табл. 1 при соответствующих реакционных сериях.

 

Вычисление потенциалов полуволн полярографического восстановления. В табл. 10 находят соответствующий класс соединений, номер корреляционного уравнения и значения постоянных, характеризующих данную серию. В преамбуле к табл. 8 находят корреляционное уравнение, а по табл. 3–7 определяют значения постоянных для заместителей. Затем производят расчет по корреляционному уравнению, как было указано выше.

Приведем примеры пользования таблицами.

Пример 1. Пусть нас интересует константа диссоциации п-нитробензойной кислоты в 70%-ном этаноле.

Основная реакционная серия диссоциации карбоновых кислот имеет индекс 1-0 (табл. 1), У соответствующей производной реакционной серии индекс 1-11 (число 11 взято из табл. 2). Реакционная серия с этим индексом и указанным растворителем приведена в табл. 8 под № 14. Здесь находим, что для расчетов следует применять уравнение (5) Гаммета, пользуясь следующими значениями постоянных: lg k_о = – 6,174; ρ = 1,738. Для п-NO₂ -группы находим в табл. 5 величину σ = 0,778.

Следовательно, искомая величина может быть вычислена по формуле:

lg K = – 6,174 + 1,738 • 0,778 = – 4,819

Учитывая величину s (табл. 8), имеем:

рK = 4,819 ± 0,127;   K = 1,52 • 10^-5

Пример 2. Требуется рассчитать условия щелочного гидролиза эквимолекулярной смеси этилацетата и трет-бутилацетата так, чтобы обеспечить гидролиз первого из них практически нацело при условии максимальной сохранности второго.

Основная серия щелочного гидролиза ацетатов X–ООС–СН₃ приведена в табл. 1 и имеет индекс 62-0. В данном случае нас интересует именно основная реакционная серия. В табл. 8 под № 200 для нее приведены данные при 35 °С в 40%-ном диоксане. Для расчетов следует применять уравнение (3), пользуясь следующими величинами: lg k₀ = –0,28; r* = 1,34; d^с = 0,730; вычисляется бимолекулярная константа k_AB. Следовательно, надо пользоваться стерическими постоянными E_s^c. В случае этилацетата Х = С₂Н₅; s* = – 0,100 (табл. 3); E_s^c = – 0,38 (табл. 4). Для трет-бутилацетата X = С(СН₃)₃; s* = – 0,300 (табл. 3); E_s^c = = – 2,46 (табл. 4). Подставляя указанные величины в уравнение (3), получим для этилацетата:

lg k = – 0,28 + 1,34 (– 0,100) + 0,730 (– 0,38) = – 0,69

k = 0,205

для трет-бутилацетата:

lg k = – 0,28 + 1,34 (– 0,300) + 0,730 (– 2,46) = – 2,48

k = 3,305•10^-3

Исходя из этих величин и пользуясь уравнениями формальной кинетики, найдем: а) при добавлении 1 моль/л эквимолекулярной смеси указанных сложных эфиров к 3М раствору NaОН в 40%-ном диоксане при 30 °С через 9–10 сек гидролизуется 99% этилацетата и 3% трет-бутилацетата, после чего необходима нейтрализация. Если нейтрализация запаздывает, то через 37 сек прореагирует 10% трет-бутилацетата и т. д.; б) при добавлении 1 моль/л эквимолекулярной смеси сложных эфиров к 0,508 моль/л NаОН через 2,5 ч прореагирует 99,9% этилацетата и 1,6% трет-бутилацетата.

Производя аналогичные расчеты, можно установить наиболее приемлемые условия гидролиза.

Пример 3. Для кеталей

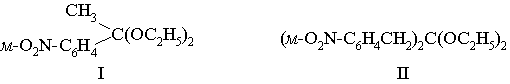
требуется вычислить устойчивость (характеризуемую периодом полупревращения) в 0,001 н. растворе НСl в 50%-ном диоксане.

Основная реакционная серия кислотного гидролиза ацеталей и кеталей имеет в табл. 1 индекс 189-0. Ему в табл. 8 соответствует № 378; здесь приведены данные при 25 °С в 49,6%-ном диоксане. Для расчетов следует применять уравнение (2а), пользуясь следующими величинами: lg k = 2,876; r* = – 3,600; h = 0,54; y = 5,13. В соединении I имеет место неполярное сопряжение одной p-электронной системы с реакционным центром; в гиперконъюгации с последним находятся три С—Н-связи метильной группы (п = 3). В стандартном соединении (ацетонале) n_о = 6, следовательно, Dn = –3. Для СН₃ s* = 0,000 (табл. 3). Для м-O₂NC₆H₄ s* вычислим, исходя из значения s^o для м-NO₂, равного 0,70 (табл. 5), по формуле, приведенной в преамбуле к табл. 3:

s* (м-O₂NC₆H₄) = 0,70 + 0,600 = 1,30

Подставляя эти значения в уравнение (2а), для бимолекулярной константы скорости гидролиза кеталя I получим:

lg k_I = 2,876 – 3,606 (0,00 + 1,30) – 3 • 0,54 + 5,13 = 1,71

В соединении II п = 4 и Dn = –2, сопряжение p-электронных систем с реакционным центром отсутствует. Величина s* для м-O₂NC₆H₄CH₂ вычисляется, исходя из s* для м-O₂NC₆H₄ (см. выше) по формуле, приведенной в преамбуле к табл. 3.

s* (м-O₂NC₆H₄CH₂) = 0,360 • 1,30 = 0,468

Следовательно, для константы скорости гидролиза кеталя II:

lg k_II = 2,876 – 3,600 (0,468 + 0,468) – 2 • 0,54 = – 1,57

Псевдомономолекулярные константы скорости при [Н⁺] = 0,001 составляют:

k_I • 0,001 = 5,13 • 10^-2;                   k_II • 0,001 = 2,7 • 10^-5

Следовательно, период полупревращения для кеталя I равен 13,4 сек, а для кеталя II – 7 ч 6 мин.

Пример 4. Необходимо рассчитать время, требуемое для получения заданного выхода продукта при синтезе соединений

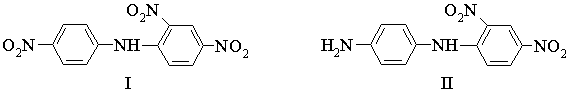
исходя из соответствующего замещенного анилина и 2,4-динитрохлорбензола.

Переменный заместитель находится в амине, следовательно, следует искать нужную основную реакционную серию в табл. 1, среди реакций для аминов, а не для нуклеофильных замещений в ароматическом ряду. Индекс основной реакционной серии 148-0, в производной серии нужно заменить 0 индексом для Z = фенилен (табл. 2) — 148-11. В табл. 8 этому индексу соответствует № 328. Приведены данные для этанольного раствора при 25 и 100 °С, что позволяет вычислить k_AB для любой температуры с помощью уравнения Аррениуса. Для расчетов следует применять уравнение (5а), пользуясь следующими величинами. Для п-NO₂ s ^– = 1,270 (табл. 5), для п-NH₂     s ^– = – 0,66 (табл. 5). Подставляем эти величины и приведенные в табл. 8 значения  lg k и r в уравнение (5а) и вычисляем значения бимолекулярной константы скорости. После интерполяции по уравнению Аррениуса получим:

для соединения I  при 80 °С

lg k_I = – 3,06 – 3,12 • 1,27 = –7,02;                 k_I = 9,5 • 10^–8 л • моль/сек

для соединения II  при 25 °С

lg k_II = – 3,952 + 3,976 • 0,66 = – 1,33;           k_II = 4,7 • 10^–2 л • моль/сек

Следовательно, если взять для синтеза соединения I этанольный раствор, 3М по п-нитроанилину и 1М по 2,4-динитрохлорбензолу, то для получения 90%-ного выхода (от теоретического) нужно кипятить смесь с обратным холодильником в течение 112 суток, а для 50%-ного выхода – в течение 34 суток.

Для получения 99%-ного выхода (от теоретического) соединения II достаточно выдержать этанольный раствор 1М как по п-фенилендиамину, так и по 2,4-динитрохлорбензолу, в течение 35 мин при 25 °С.

 

2. Полуэмпирическая схема Q-e

Для количественной оценки реакционной способности ненасыщенных мономеров большое распространение получил предложенный Алфреем и Прайсом полуэмпирический метод – схема Q-e, позволяющий связать кинетические характеристики бинарной сополимеризации со структурными параметрами мономеров.

Кинетическая схема сополимеризации. Процесс сополимеризации включает те же стадии, что и полимеризация одного мономера: инициирование, рост цепи, обрыв и передача цепи. Однако описание этих стадий существенно усложняется, поскольку с увеличением числа сомономеров резко увеличивается число элементарных реакций на каждой стадии.

Наиболее важной с точки зрения химического строения сополимеров является стадия роста цепи. Эта стадия полностью определяет состав сополимера и последовательность мономерных звеньев в его макромолекулах. Число реакций роста, которые необходимо учитывать в кинетической схеме сополимеризации, зависит от числа сомономеров и от числа отличающихся реакционной способностью активных центров. Это положение является общим для всех механизмов сополимеризации.

В большинстве случаев реакционноспособность растущего активного центра (макрорадикала, макрокатиона или макроаниона) определяется строением концевого мономерного звена и не зависит от природы предшествующих звеньев (модель концевого звена).

Иногда требуется учет эффекта предпоследнего звена (модель предконцевого звена ) и более удаленных звеньев, что ведет к увеличению числа различающихся активных центров и, соответственно, к увеличению числа реакций роста цепи. Эффект предпоследнего звена наблюдается достаточно редко как в радикальной, так и в ионной сополимеризации. В радикальных процессах он проявляется в системах, включающих мономеры с объемными и полярными заместителями, например, при сополимеризации фумаронитрила со стиролом.

Кинетическая схема бинарной сополимеризации мономеров М₁ и М₂ с использованием модели концевого звена включает следующие элементарные реакции роста цепи:

   Реакция                       Скорость реакции

                 ( I )

                ( II )

                  ( III )

                ( IV )

где  m₁* и m₂* – растущие активные центры с концевыми звеньями мономеров M₁ и М₂, соответственно;

k₁₁, k₂₂ – константы скоростей реакций гомогенного роста цепи;

k₁₂, k₂₁ – константы скоростей перекрестного роста (первая цифра индекса относится к активному центру, вторая – к мономеру).

Константами сополимеризации или константами относительной активности мономеров являются величины r₁ = k₁₁/k₁₂ и r₂ = k₂₂/k₂₁, характеризующие отношение констант скоростей взаимодействия мономеров М₁ и М₂ с одним и тем же активным центром.

Константы r₁ и r₂ зависят от химической природы сомономеров и для каждой пары М₁ и М₂ имеют свои собственные значения: от нуля (если преобладает перекрёстный рост цепи, т.е. k₁₂ >> k₁₁ или k₂₁ >> k₂₂) и до величин, значительно превышающих единицу (при k₁₁ >> k₁₂ или k₂₂ >> k₂₁).

Константы сополимеризации являются важнейшими характеристиками процесса. Они определяют зависимость состава сополимера от состава мономерной смеси в соответствии с дифференциальным уравнением сополимеризации:

 

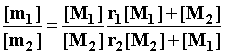
где [m₁] и [m₂] – содержание мономерных звеньев М1 и М2 в сополимере, выражаемое в тех же единицах, что и концентрации мономеров [M₁] и [M₂] в исходной смеси (в мольных долях, мол.% или в молях).

Дифференциальное уравнение сополимеризации справедливо при небольшой глубине превращения.

Известно, что связь между структурой и реакционной способностью органического соединения определяется резонансными, полярными и стерическими факторами. Схема Q-e, предложенная Алфреем и Прайсом, является попыткой количественной оценки роли первых двух.

В основе метода лежит допущение о том, что константу скорости присоединения радикала i к мономеру j:

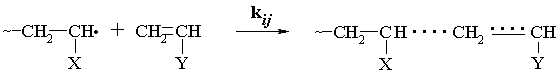
можно представить в виде

k_ij = P_iQ_j exp(-e_ie_j)                              (1)

где Р – параметр реакционной способности растущего радикала;

Q – резонансный параметр мономера, отражающий степень сопряжения заместителя с реакционным центром (Q = exp{-q/RT}, где q – энергия сопряжения в переходном состоянии);

е – фактор полярности, значение которого обусловлено поляризующим влиянием заместителя на реакционный центр в мономере или в радикале (при этом мономеру и соответствующему ему радикалу приписывается одна и та же величина е). Считается, что e = e / (rDRT)^1/2, где e – заряд на атоме, образующем связь, и обусловленный влиянием заместителя (X или Y); r – расстояние между атомами в переходном состоянии; D – диэлектрическая проницаемость.

Электронодонорные заместители характеризуются отрицательными значениями е, а электроакцепторные – положительными.

Константы сополимеризации с учетом уравнения (1) определяются через структурные факторы:

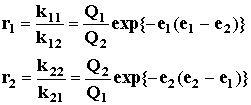         (2)

 

 

Для стирола условно принято Q = 1,0 и е =  – 0,8. Относительные величины Q и е для других мономеров определяют из экспериментальных значений r₁ и r₂ по уравнениям:

                             (3)

            (4)

Несмотря на эмпирический и приближенный характер схемы Q-е, на ее основе можно успешно предсказывать значения констант сополимеризации, а также определять резонансную и полярную составляющие реакционной способности мономеров.

При сополимеризации мономеров, не проявляющих полярный эффект (е₁= е₂ = 0), выражения (2) приобретают вид: r₁ = Q₁/Q₂, r₂= Q₂/Q₁ и произведение констант сополимеризации будет равно единице. Это свидетельствует о равном вкладе реакций гомоприсоединения и перекрестного роста цепи и отражает случай "идеальной" сополимеризации, при которой активность мономеров определяется только фактором сопряжения, а распределение звеньев в макромолекуле носит статистический характер.

В случае сополимеризации мономеров, содержащих противоположные по направлению поляризации заместители (например, е₁< 0 < е₂), полярный эффект оказывает существенное влияние и на скорость реакции, и на строение сополимера. При этом произведение констант сополимеризации

r₁r₂= exp{-(e₁-e₂)}²                              (5)

стремится к нулю, что отражает тенденцию к чередованию мономерных звеньев за счет преобладания реакций перекрестного роста. Полярный эффект может способствовать вовлечению в сополимеризацию малоактивных мономеров. Например, не склонный к гомополимеризации по радикальному механизму винилбутиловый эфир (Q = 0.03; e = -1.4) вступает в сополимеризацию с электроноакцепторными мономерами, в частности с винилхлоридом (е = 0.2), по-видимому, вследствие понижения энергии переходного состояния, стабилизированного электростатическим взаимодействием реагирующих частиц:

Соединения, характеризующиеся отрицательными значениями е, как правило, хорошо полимеризуются по катионному механизму, а положительными – по анионному.

Необходимо отметить, что при ионной полимеризации реакционная способность мономеров обычно согласуется с полярным фактором строения. Это отражается в соблюдении правила Гаммета-Тафта, которое применительно к ионной сополимеризации можно записать в виде:

 

lg 1/r₁ = ρσ                                    (6)

 

где σ – константа заместителя при двойной связи, характеризующая его электронодонорные или электроноакцепторные свойства (между σ и e Алфрея-Прайса удовлетворительно выполняется линейная зависимость);

ρ – константа реакционной серии М₁-М_i, связанная с механизмом реакции и ее чувствительностью к полярному эффекту заместителей в мономерах М_i.

Как показывают данные по сополимеризации стирола (М₁) с его производными CH₂=CH-C₆H₄X (M_i), где X = CH₃, CH(CH₃)₂, OCH₃, Cl, NO₂ и др., ρ имеет положительные значения для анионных и отрицательные – для катионных процессов.